SPFA 的各类玄学优化大全

绝大部分算法来源于网络，部分算法我没有找到 hack。

有些算法可能被卡到指数级，不要在正式比赛使用

众所周知，带优化的 SPFA 时间复杂度为：O(玄学)

-1. AVX 指令集常数优化

_mm512_i64gather_epi64 并行取变量值

_mm512_add_epi64 并行加

_mm512_min_epi64 并行取最小值

_mm512_i64scatter_epi64 并行赋值

照这么看的话，还真的可以用 avx 优化，不过我没有实际测试过

1. LLL

每次将出队结点距离和队内距离平均值比较，如果更大则插入至队尾。

Hack：向 1 连接一条权值巨大的边，这样 LLL 就失效了。

2. SLF

常用的算法之一，每次将入队结点距离和队首比较，如果更大则插入至队尾。这个算法在负权图上，有可能被卡到指数级，不建议单独使用。

Hack：使用链套菊花的方法，在链上用几个并列在一起的小边权边就能欺骗算法多次进入菊花。

3. SLF 带容错

每次将入队结点距离和队首比较，如果比队首大超过一定值则插入至队尾。

Hack：开大边权

4. mcfx 优化

据说来自于知乎用户 mcfx

在第 [L,R] 次访问一个结点时，将其放入队首，否则放入队尾。通常取 L=2, R=sqrt(n)。

Hack：菊花图表现很差。

5. NTR

来源：知乎

维护一个叫临时最短路树的东西，刚开始只有一个源节点这SPFA的过程中，每次松弛(u, v)边时将v的父亲设为u；v是有可能有后代的，所以将其所有后代的对应inqueue标记清除；在SPFA过程中如果发现队头节点的inqueue为空那么跳过。理由是如果我们能松弛(u, v)边，那么从(u, v)走势必比以前走过的那种走法好。将这个步骤称为NTR。

6. swap

每当队列改变时，如果队首距离大于队尾，则交换首尾。

7. 阈值 swap

来源：csdn

首先设置一个阈值t，初始化为1。对每个节点x记录所执行过的松弛操作的次数。每次从队头取出元素x时，若这个次数大于t，就把x丢入队尾，同时增大阈值t，不执行任何其他操作。

8. 概率排序

队列长度为 len，每次操作有 1/(len+1) 的概率触发排序（按 dis 排序）

9. 堆

正权图上很快（但是意义不大，因为可以用 dijkstra），负权图上可能退化到指数级，不推荐使用

10. 栈

最坏时间复杂度仍然为指数级，不推荐使用

11. 随机化

每次将队首与队内随机一个值交换（相当于随机出边），这样你就得到了一个玄学复杂度的算法，可能很快也可能很慢。但是可以被卡。

12. 无用边优化

这个东西是我研究出来的，可以对付一些很特殊的数据。在一般的图上，几乎没有什么用。

对于一条边，如果他是一条死路（不可能达到终点），就将它删除。如果某个点的入度和出度都为 1，就压缩路径。

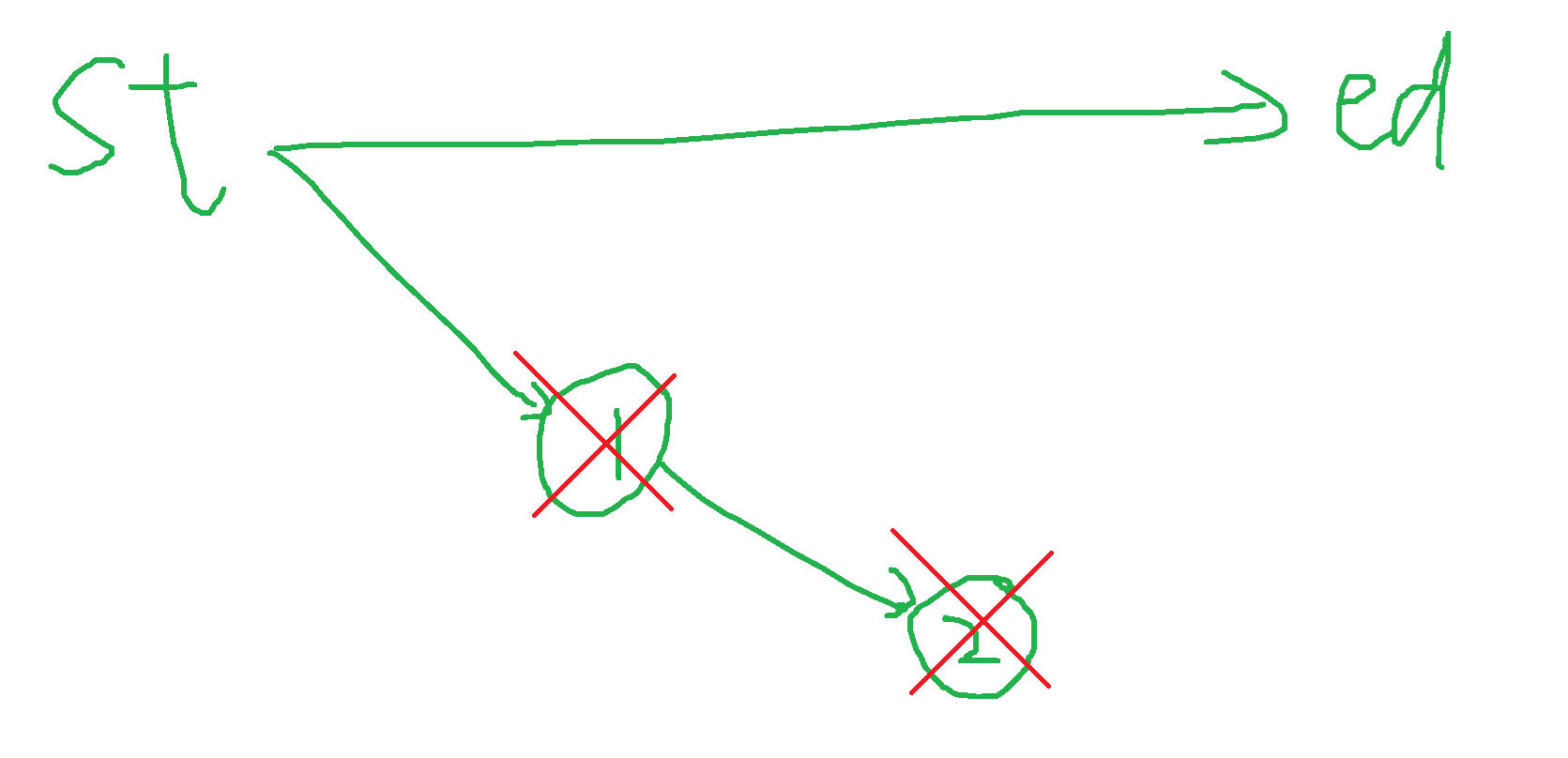
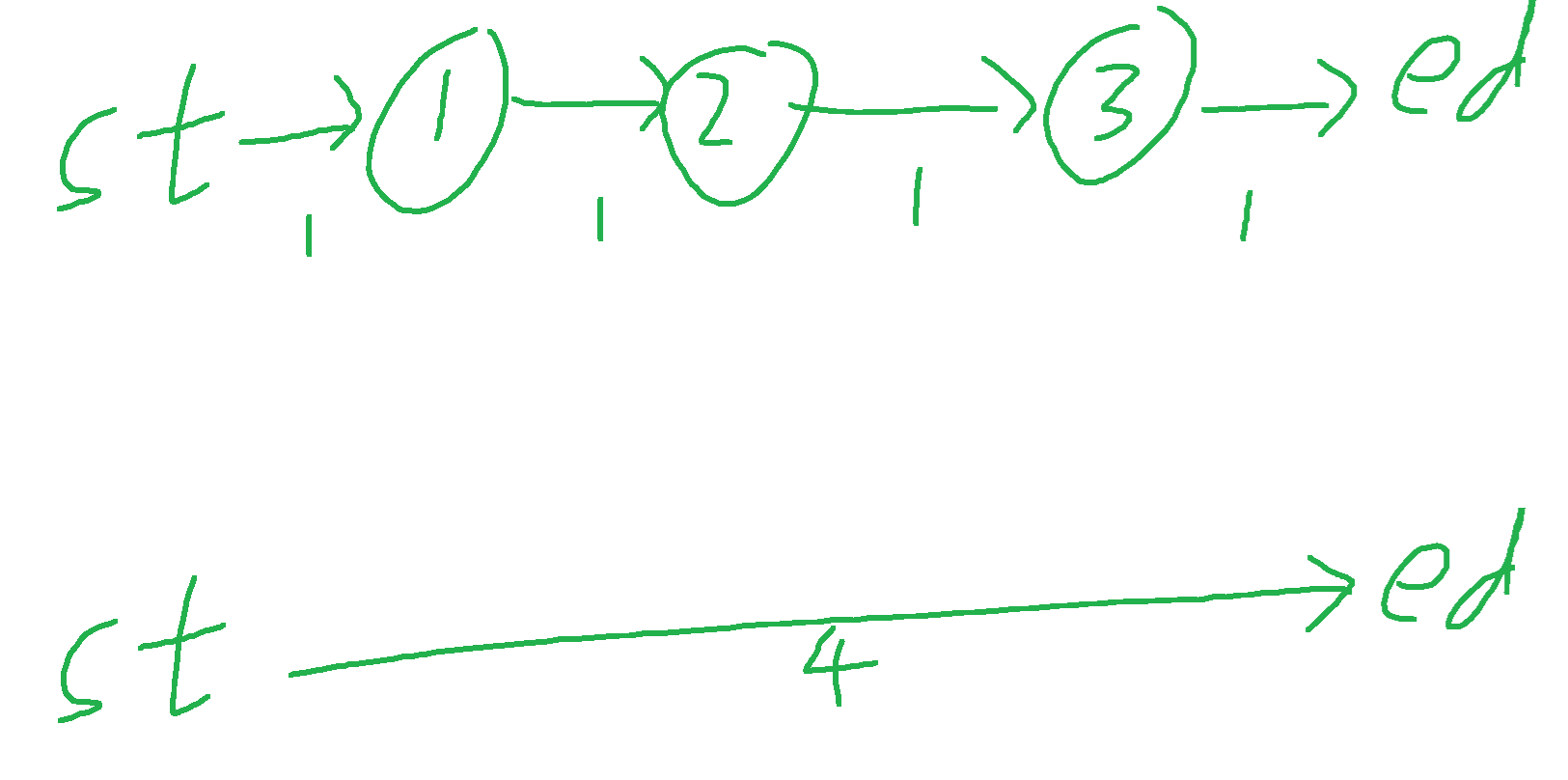
Hack：给每个点都向终点连一条权值巨大的边。当然 Hack 方法还有很多。

附录 A：卡 spfa 数据构造器

经实际测试，可以卡掉标准 spfa，但是奇奇怪怪的 spfa 可能卡不掉。

mt19937 rnd(time(0));
void make1() { // 随机图
	const int n=200000, m=500000;
	printf("%d %d\n",n,m);
	for(int i=1; i<=m; i++) printf("%d %d %d\n",rnd()%n+1,rnd()%n+1,rnd()%2000000001-1000000000);
}
void make2() { // 标准链套菊花图
	const int n=200000,m=2*n-3;
	printf("%d %d\n",n,m);
	for(int i=n; i>=2; --i) printf("1 %d %d\n",i,(n-i+1)*2+1), printf("%d %d 1\n",i,i-1);
}
void make3() { // 网格图
	const int n=90000; // 300*300
	int m=299*300*2+300*299*2+299*299;
	printf("%d %d\n",n,m);
	for(int i=1; i<=300; ++i)
		for(int j=1; j<=300; ++j) {
			if(i<300) {
				printf("%d %d 1\n", (i-1)*300+j, (i)*300+j);
				printf("%d %d 1\n", (i)*300+j, (i-1)*300+j);
				if(j<300) {
					printf("%d %d %d\n", (i-1)*300+j, (i)*300+j+1, rnd()%100000+10);
				}
			}
			if(j<300) {
				printf("%d %d %d\n", (i-1)*300+j, (i-1)*300+j+1, rnd()%100000+10);
				printf("%d %d %d\n", (i-1)*300+j+1, (i-1)*300+j, rnd()%100000+10);
			}
		}
}
void make4() { // 另一种链套菊花图
	const int n = 1000;

	printf("%d %d\n",n,(n-1+(n-1)*(n-2)/2));

	for(int i=2; i<=n; i++)
		printf("1 %d %d\n",i,3000-((i-2)*2));

	for(int i=3; i<=n; i++) {
		for(int j=2; j<i; j++) {
			printf("%d %d %d\n",i,j,2*(i-j)-1);  //让前面的点反复进出队列，使spfa超时
		}
	}
}